Матеріали до уроку 4
1. Теоретичний матеріал
Точка, що лежить на прямій, ділить пряму на дві частини, кожна з яких називається променем, що виходить із цієї точки. Цю точку називають початком кожного з променів.
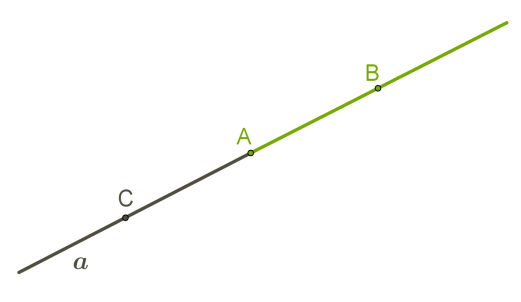
Точка A ділить пряму a на два промені. Оскільки важливо розуміти, який із променів розглядаємо, поставимо на прямій іще дві точки: B і C . Назвемо промені: промінь AB і промінь AC .
Зверни увагу!
Першою завжди називають початкову точку променя.
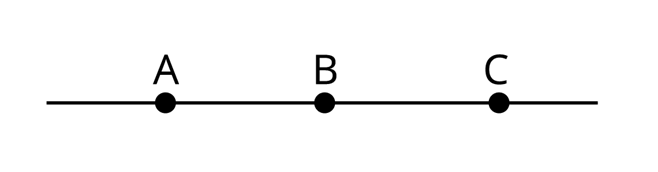
На цьому рисунку кожна з точок може бути початковою точкою певного зображеного променя. З кожної точки виходять два промені в протилежні напрямки і, подібно до прямої, продовжуються нескінченно.
Зверни увагу!
Промінь BC — той самий промінь AC, але промінь BC відрізняється від променя AC. Ці промені мають певну спільну частину.
Два різні промені однієї прямої зі спільною початковою точкою називаються доповняльними променями.
Зверни увагу!
Об'єднавши промені СА та АС, ми також отримаємо пряму АС. Проте ці промені не є доповняльними: у них немає спільного початку.
Кут — геометрична фігура, яка складається з точки і двох променів, що виходять із цієї точки. Ці промені називають сторонами кута, а їхній спільний початок — вершиною кута.
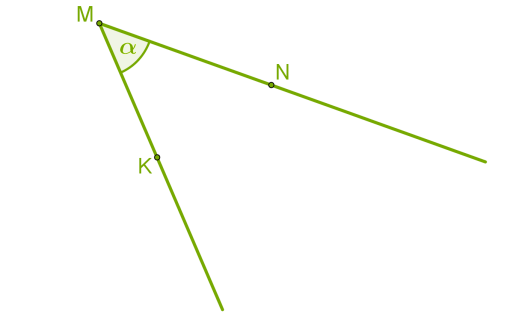
Кут позначають великими латинськими буквами, наприклад, ∠KMN , або малими грецькими буквами, наприклад, α .
Зверни увагу!
Кут ∠KMN можна назвати також ∠NMK , але буква, що позначає вершину, завжди пишеться посередині.
Іноді кут можна позначити тільки однією великою латинською буквою вершини, цифрою або назвами променів — малими латинськими буквами, наприклад, ∠M , ∠1 або ∠mn .
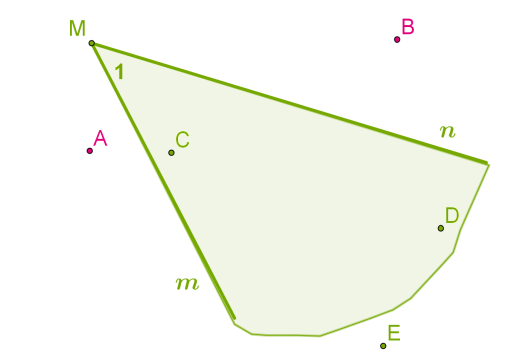
Промені n і m зі спільним початком у точці M ділять площину на дві частини: внутрішню і зовнішню область кута.
Кутом також можна називати промені зі спільним початком разом із внутрішньою областю. Тоді точки A і B не належать куту ∠M , а точки C, D і E належать куту ∠M .
Якщо провести два промені, що виходять із однієї точки, то внутрішня область утворює один кут, а зовнішня область — інший.
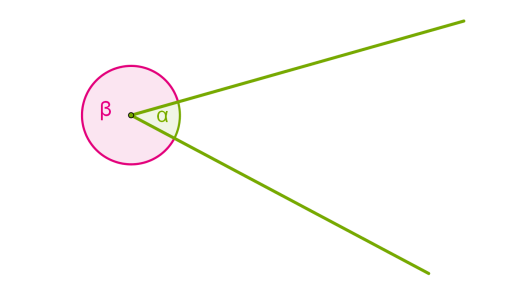
Якщо обидві сторони кута лежать на одній прямій, кут називається розгорнутим.
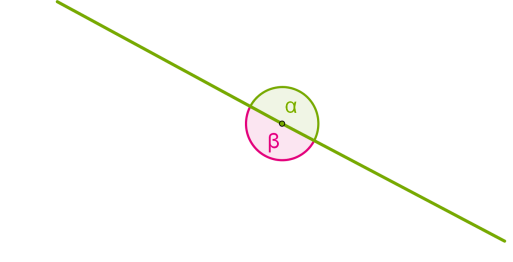
Внутрішньою областю розгорнутого кута можна вважати будь-яку з двох частин, на які він ділить площину.
Якщо у внутрішній області кута провести промінь із початком у вершині цього кута, то промінь поділить кут на два кути.
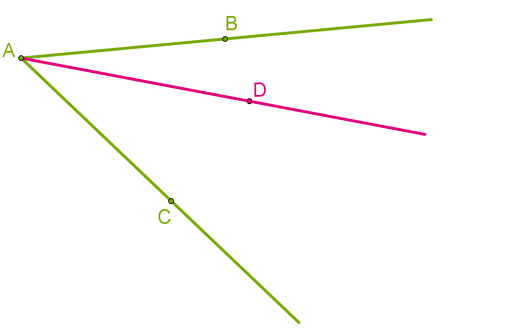
У такому випадку важливо правильно називати кути, оскільки ми маємо даний кут і дві його частини.
Наприклад, не зовсім зрозуміло, про який кут ідеться, якщо записано ∠A . Краще використовувати три великі букви, тоді назви кутів будуть зрозумілі: ∠CAB , ∠CAD , ∠DAB .